Pivot The System About The Element Calculator
Pivot the system about the element calculator. This imparts computational stability to the algorithm. All variables should be non-negative ie. Calculus questions and answers.
Answer by MathLover1 18923 Show Source. Chapter 2 discusses Gaussian elimination. Phenolphthalein 125 mL Erlenmeyer flask 25 mL pipet and bulb pH metre acetic.
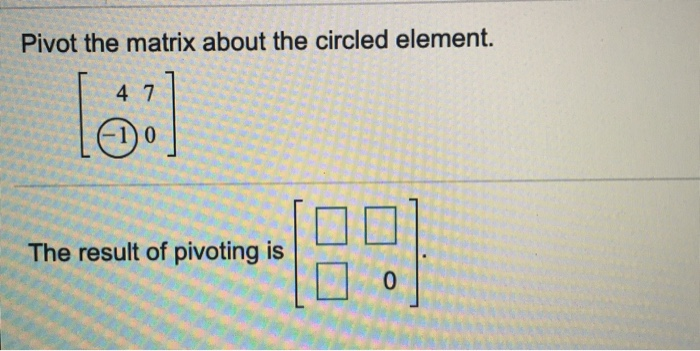
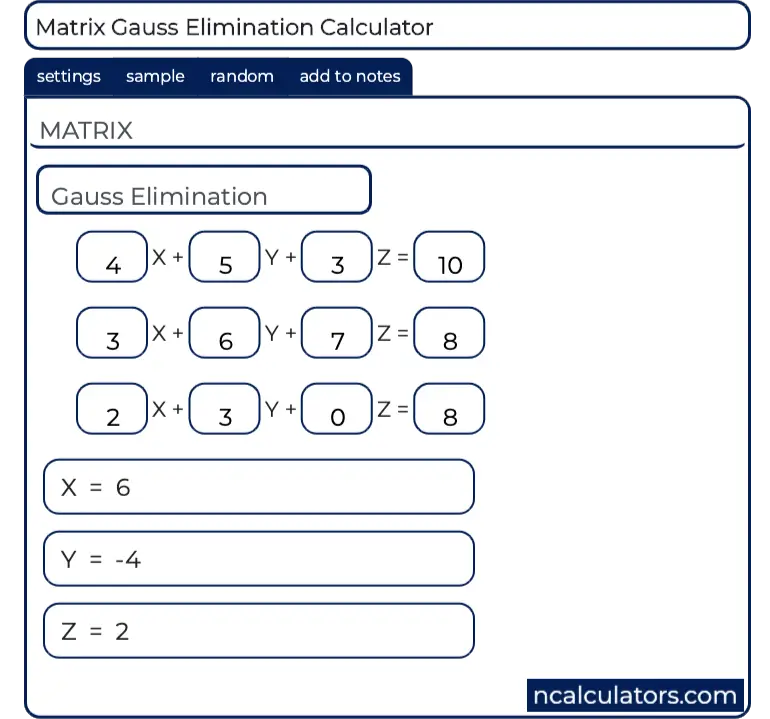
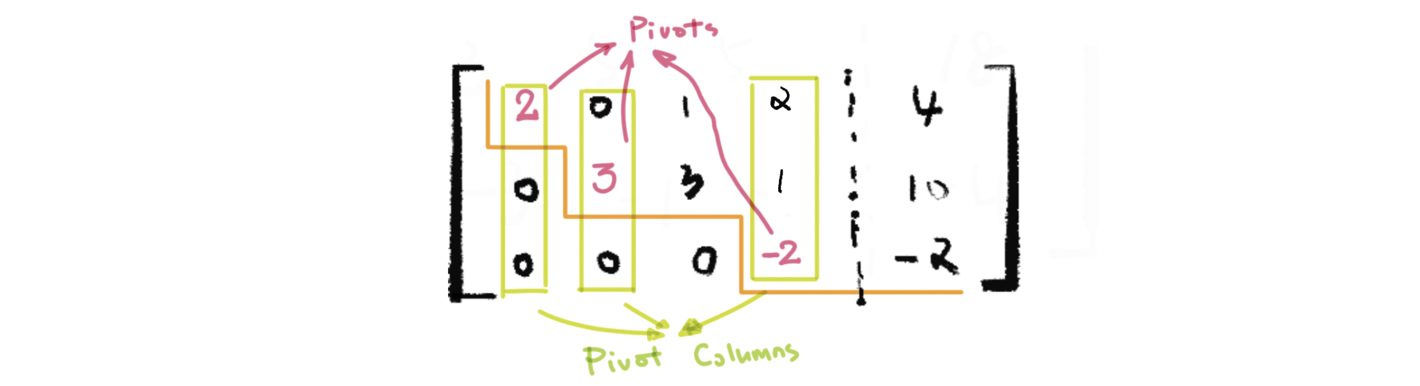
The purpose of this experiment is to determine the molar concentration of a sample of acetic acid and to calculate its Ka. Pivot the system about the element in row 2 column 2. A pivot position in a matrix is a location that corresponds to a leading 1 in its reduced echelon form.
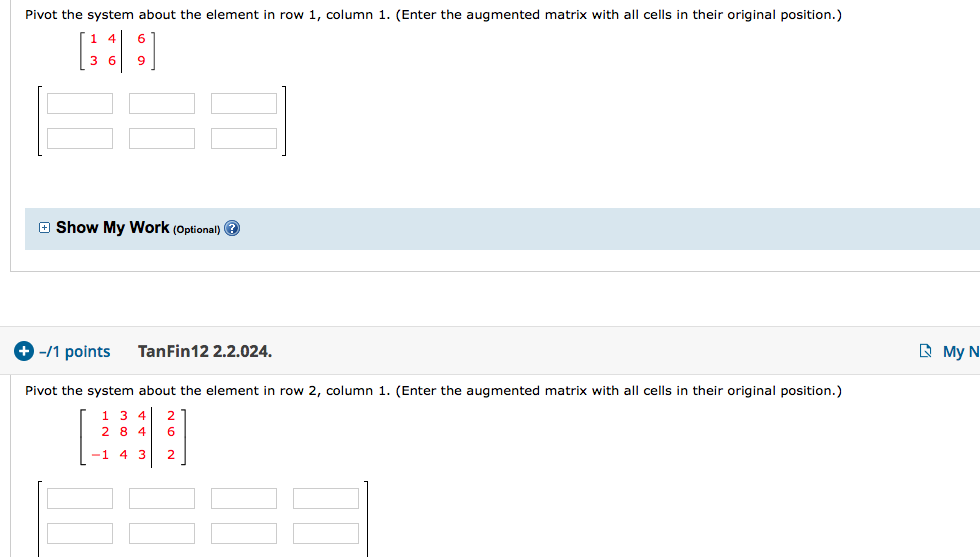
Pivot the system about the element in row 1 column 1. Assume the entire budget will be used bWrite the system of equations as an augmented matrix. Check if the linear programming problem is a standard maximization problem in standard form ie if all the following conditions are satisfied.
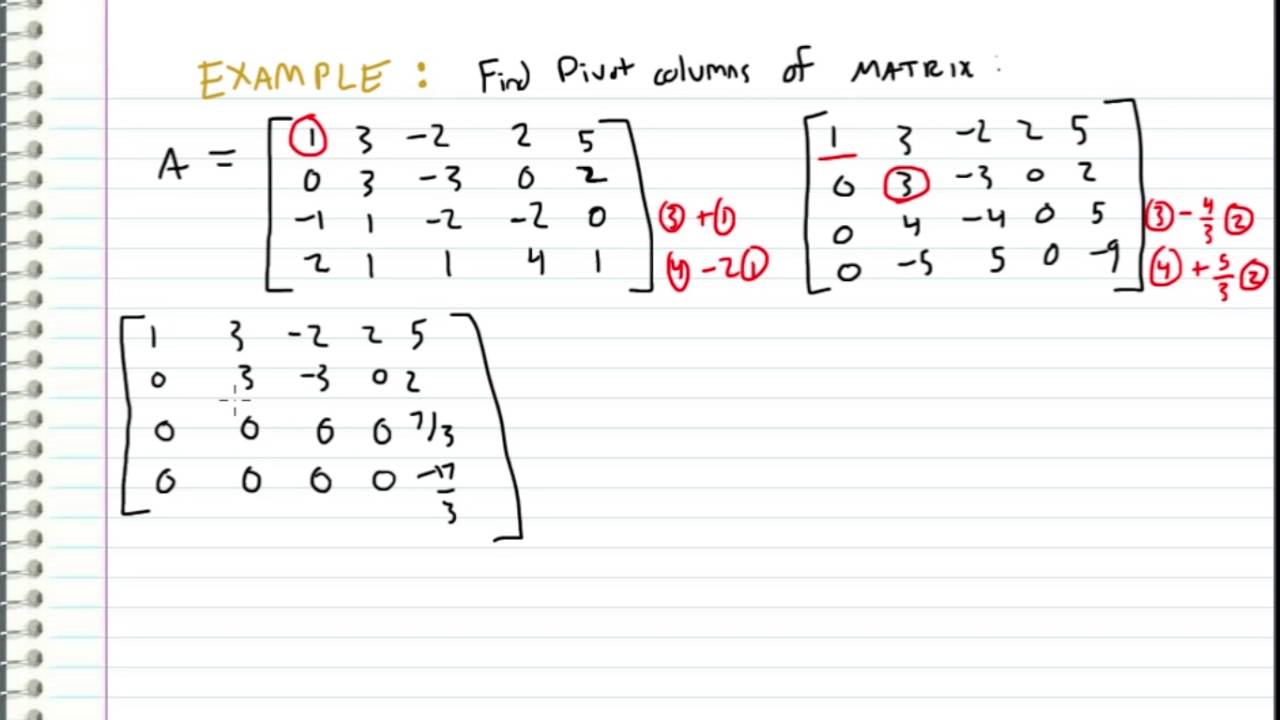
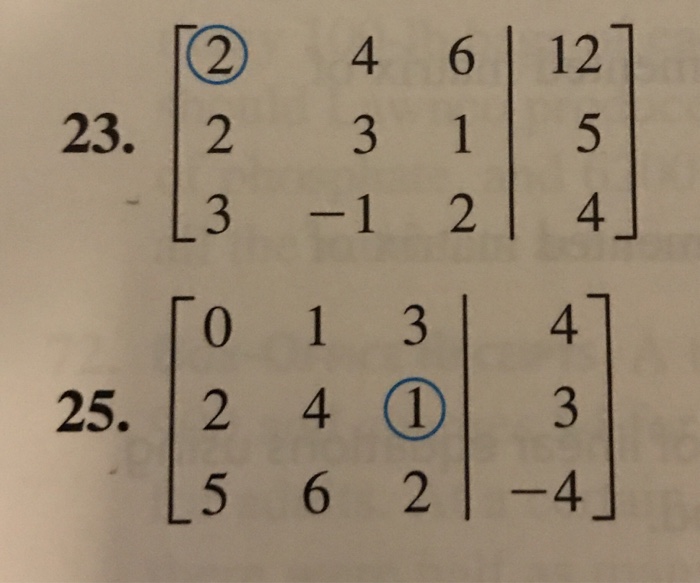
A pivot position in a. Area in acres. Pivot positions lie in columns corresponding to dependent variables for the associated systems.
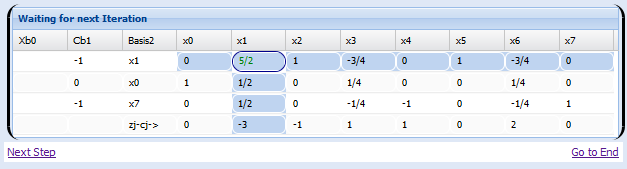
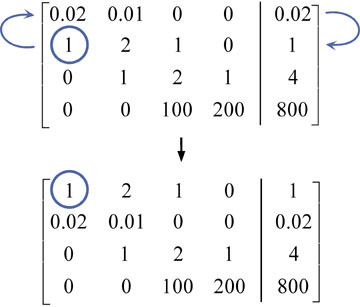
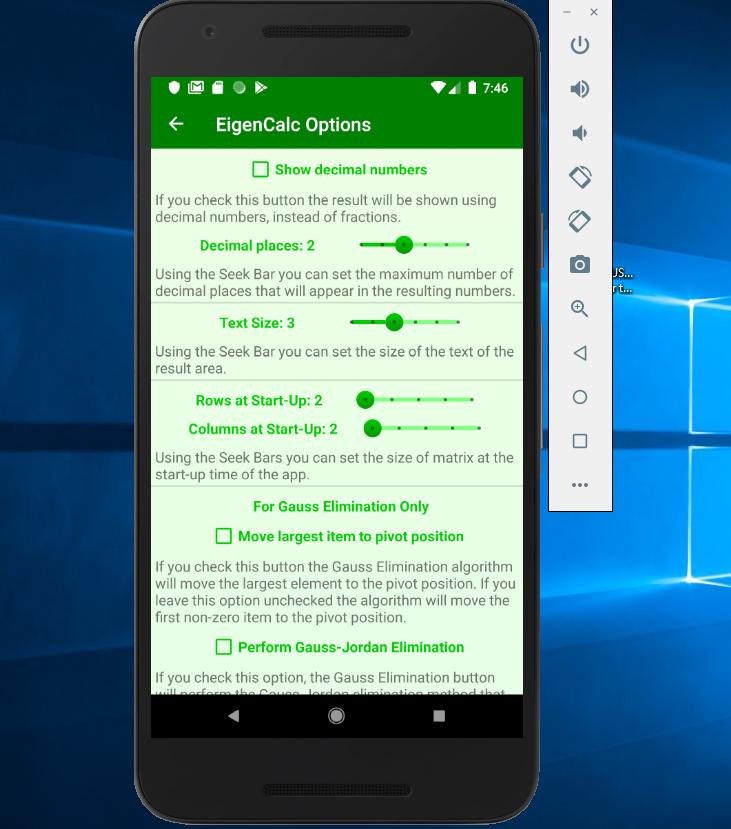
During the process if a 0 is encountered in the pivot position a row exchange solved the problemAs we will see in Chapter 11 Gaussian elimination can perform very poorly unless we incorporate row exchange into the algorithm so that the pivot a ii is the element of largest. DSolve the system of equations from here. 0 10 8 5.
If you liked my science video yo. To Begin select the number of rows and columns in.
We can solve this in O log N time through a divide-and-conquer approach which is similar to peak finding algorithm.
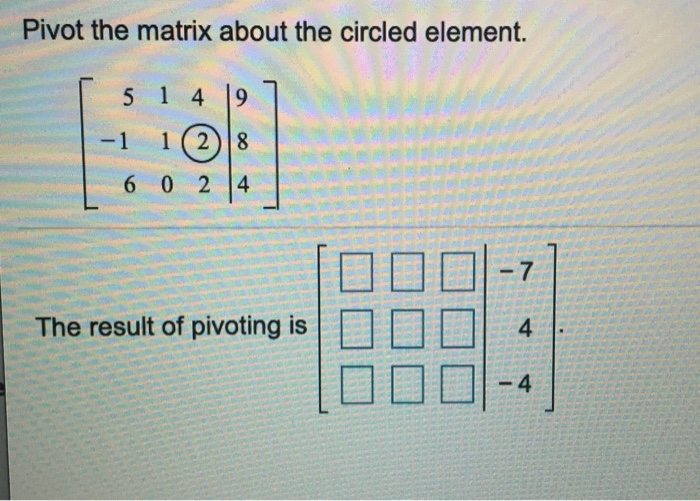
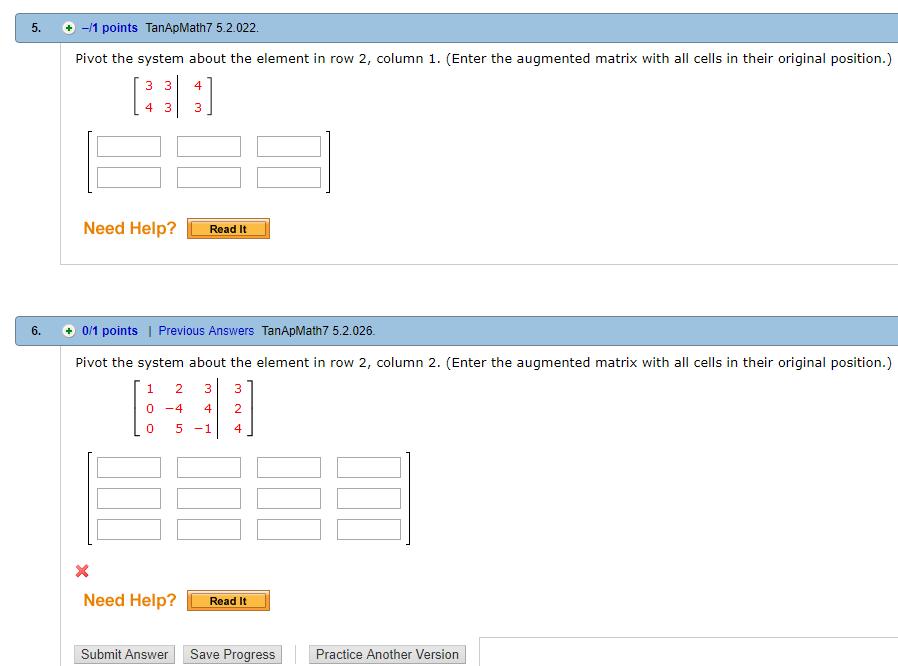
A pivot position in a matrix is a location that corresponds to a leading 1 in its reduced echelon form. Pivot points are found by a simple calculation which involves the openhighlow and close. Enter the augmented matrix with all cells in their original position Question. Pivot the system about the element in row 2 column 2. The purpose of this experiment is to determine the molar concentration of a sample of acetic acid and to calculate its Ka. To avoid division by zero swap the row having the zero pivot with one of the rows below it. Its to maximize an objective function. Pivot the system about the element in row 2 column 1. Pivot the system about the element in row 2 column 1.
Calculate the magnitude of the torque due to gravitational force around this pivot point when the string makes a 5 Thermodynamics A 30 m vertical column of fluid density 1878kgm 3. Pivot the system about the element in row 1 column 1. Do not completely reduce the matrix. Enter the augmented matrix with all cells in their original position 1 4 5 3 6 9 2. Its to maximize an objective function. Assume the entire budget will be used bWrite the system of equations as an augmented matrix. Answer by MathLover1 18923 Show Source.



















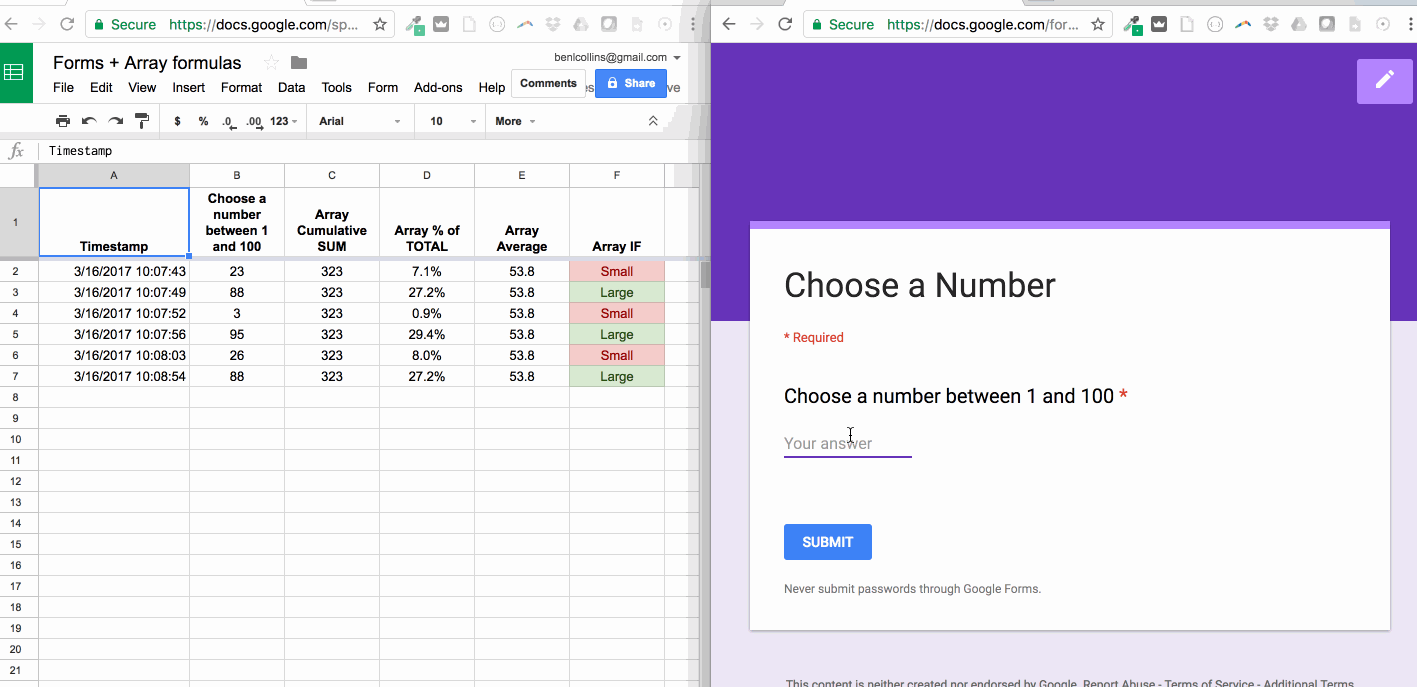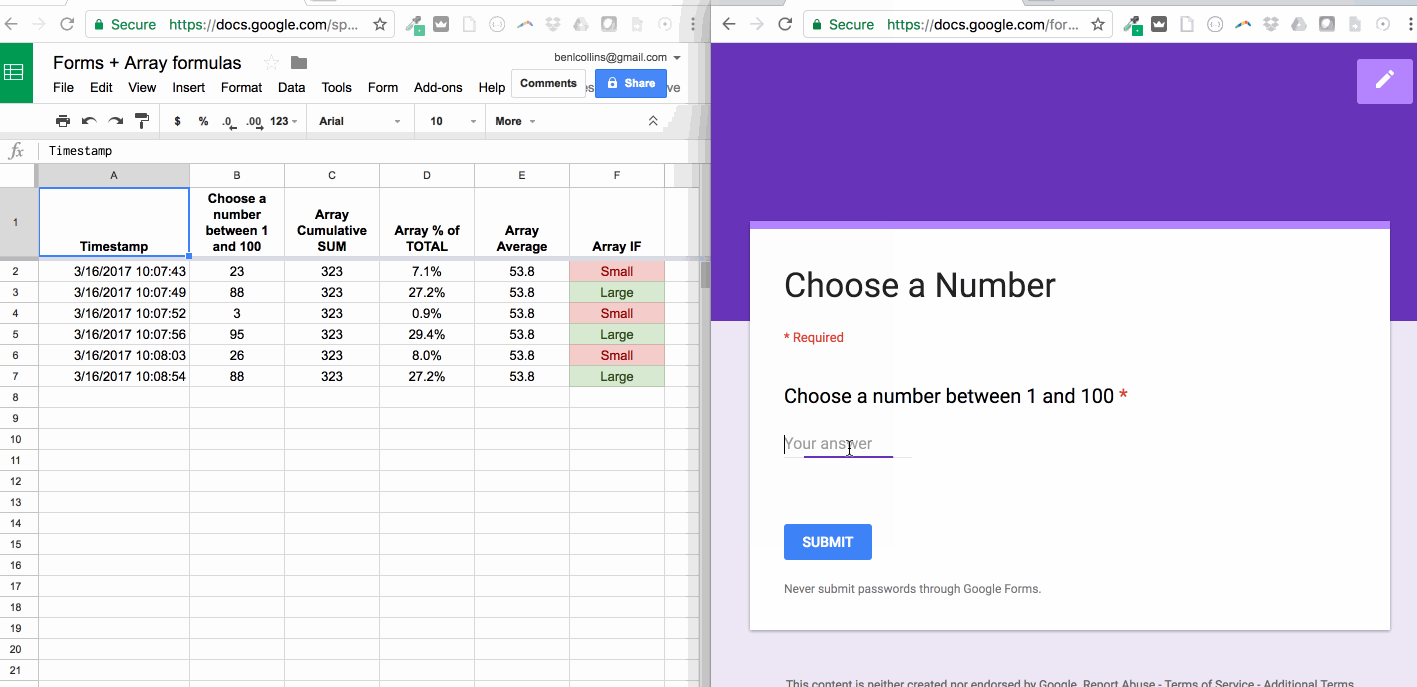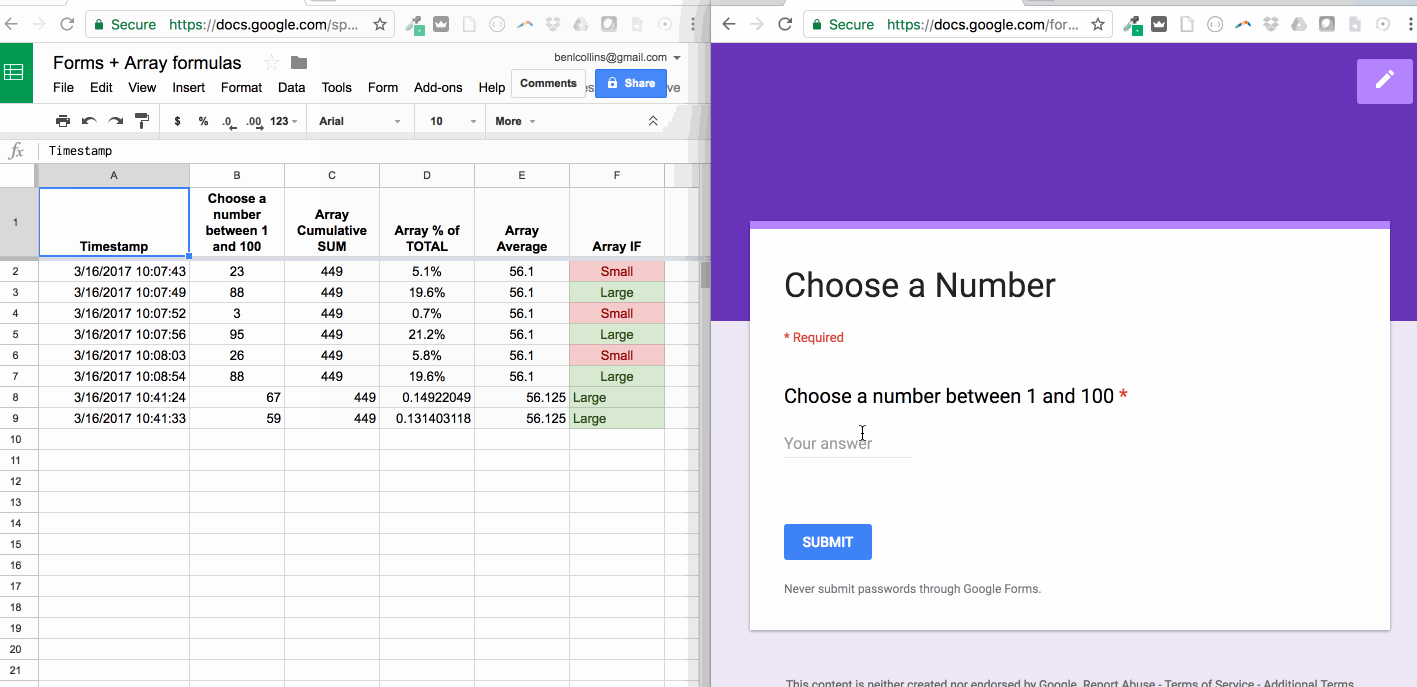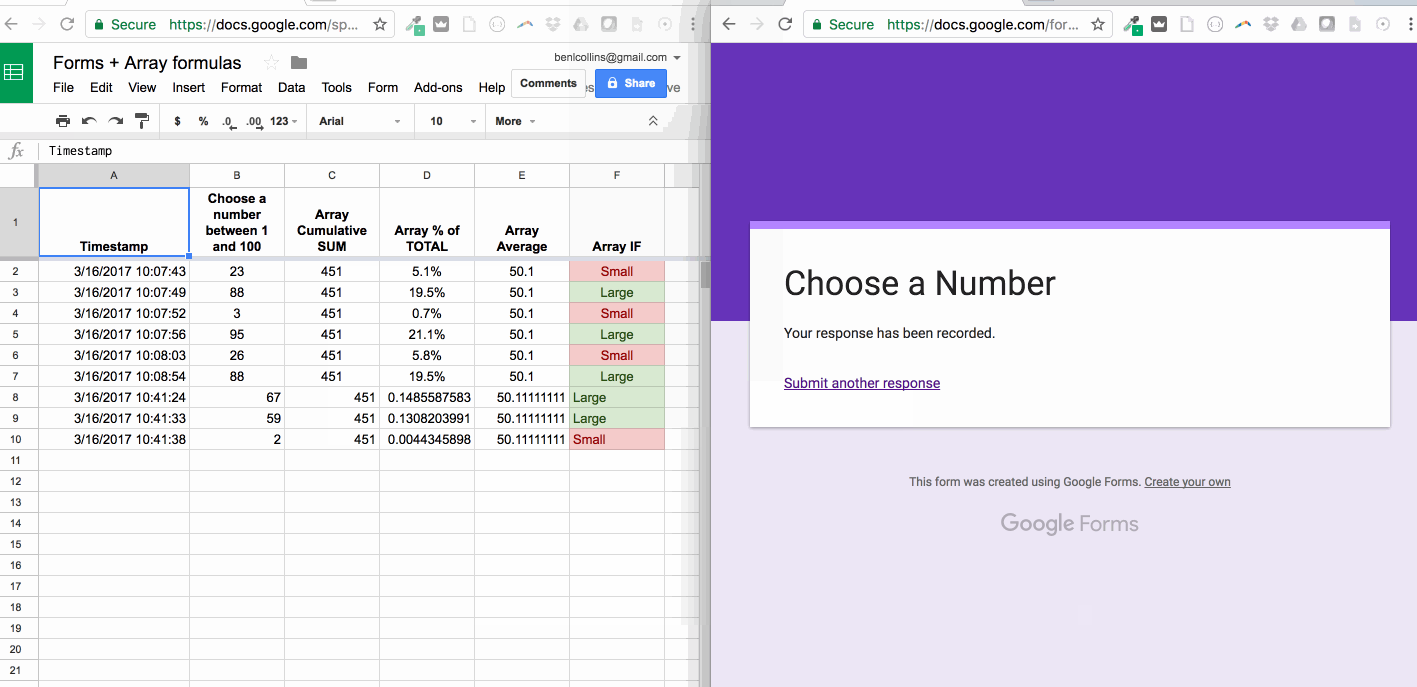



Post a Comment for "Pivot The System About The Element Calculator"